Introduction to Java Programming and Data Structures, 11E, Y. Daniel Liang

Chapter 28 Check Point Questions

Section 28.2

▼28.2.1

What is the famous Seven Bridges of Königsberg problem?

▼28.2.2

What is a graph? Explain the following terms: undirected graph, directed graph, weighted graph, degree of a vertex, parallel edge, simple graph, complete graph, connected graph, cycle, subgraph, tree, and spanning tree.

▼28.2.3

How many edges are in a complete graph with 5 vertices? How many edges are in a tree of 5 vertices?

▼28.2.4

How many edges are in a complete graph with n vertices? How many edges are in a tree of n vertices?

Section 28.3

▼28.3.1

How do you represent vertices in a graph? How do you represent edges using an edge array? How do you represent an edge using an edge object? How do you represent edges using an adjacency matrix? How do you represent edges using adjacency lists?

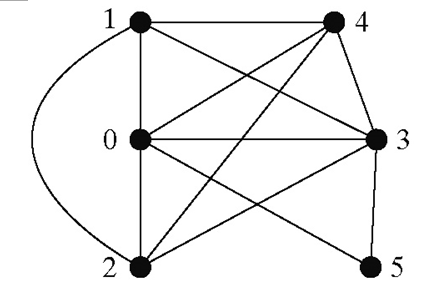
▼28.3.2

Represent the following graph using an edge array, a list of edge objects, an adjacency matrix, an adjacency vertex list, and an adjacency edge list, respectively.

Section 28.4

▼28.4.1

Describe the relationships between Graph, UnweightedGraph, and WeightedGraph.

▼28.4.2

For the code in Listing 28.2, TestGraph.java, what is graph1.getIndex("Seattle")? What is graph1.getDegree(5)? What is graph1.getVertex(4)?

▼28.4.3

Show the output of the following code.

public class Test {
  public static void main(String[] args) {
    Graph<Character> graph = new UnweightedGraph<>();
    graph.addVertex('U');
    graph.addVertex('V');
    int indexForU = graph.getIndex('U');
    int indexForV = graph.getIndex('V');
    System.out.println("indexForU is " + indexForU);
    System.out.println("indexForV is " + indexForV);
    System.out.println("Degree of U is " + 
      graph.getDegree(indexForU));
    System.out.println("Degree of V is " + 
      graph.getDegree(indexForV));
  }
}

▼28.4.4

What will getIndex(v) return if v is not in the graph? What happens to getVertex(index) if index is not in the graph? What happens to addVertex(v) if v is already in the graph? What happens to addEdge(u, v) if u or v is not in the graph?

Section 28.5

▼28.5.1

Will Listing 28.7 DisplayUSMap.java work, if the code in lines 38-42 in Listing 28.6 GraphView.java is replaced by the following code?

if (i < v) {
  double x2 = graph.getVertex(v).getX();
  double y2 = graph.getVertex(v).getY();

  // Draw an edge for (i, v)
  getChildren().add(new Line(x1, y1, x2, y2)); 
}

▼28.5.2

For the graph1 object created in Listing 28.1, TestGraph.java, can you create a GraphView object as follows?

    GraphView view = new GraphView(graph1);

Section 28.6

▼28.6.1

Does UnweightedGraph<V>.SearchTree implement the Tree interface defined in Listing 25.3 Tree.java?

▼28.6.2

What method do you use to find the parent of a vertex in the tree?

Section 28.7

▼28.7.1

What is depth-first search?

▼28.7.2

Draw a DFS tree for the graph in Figure 28.3b starting from node A.

▼28.7.3

Draw a DFS tree for the graph in Figure 28.1 starting from vertex Atlanta.

▼28.7.4

What is the return type from invoking dfs(v)?

▼28.7.5

The depth-first search algorithm described in Listing 28.8 uses recursion. Alternatively, you can use a stack to implement it, as shown below. Point out the error in this algorithm and give a correct algorithm.

// Wrong version 
Tree dfs(vertex v) {
  push v into the stack;
  mark v visited;
 
  while (the stack is not empty) {
    pop a vertex, say u, from the stack
    visit u;
    for each neighbor w of u
      if (w has not been visited)
        push w into the stack; 
  }
}

Section 28.8

▼28.8.1

How is a graph created for the connected circles problem?

▼28.8.2

When you click the mouse inside a circle, does the program create a new circle?

▼28.8.3

How does the program know if all circles are connected?

Section 28.9

▼28.9.1

What is the return type from invoking bfs(v)?

▼28.9.2

What is breadth-first search?

▼28.9.3

Draw a BFS tree for the graph in Figure 28.3b starting from node A.

▼28.9.4

Draw a BFS tree for the graph in Figure 28.1 starting from vertex Atlanta.

▼28.9.5

Prove that the path between the root and any node in the BFS tree is the shortest path between the root and the node.

Section 28.10

▼28.10.1

How are the nodes created for the graph in NineTailModel?

▼28.10.2

How are the edges created for the graph in NineTailModel?

▼28.10.3

What is returned after invoking getIndex("HTHTTTHHH".toCharArray()) in Listing 28.13? What is returned after invoking getNode(46) in Listing 28.13?

▼28.10.4

If lines 26 and 27 are swapped in Listing 28.13, NineTailModel.java, will the program work? Why not?