Introduction to Java Programming and Data Structures, 11E, Y. Daniel Liang

Chapter 29 Check Point Questions

Section 29.2

▼29.2.1

For the code WeightedEdge edge = new WeightedEdge(1, 2, 3.5), what is edge.u, edge.v, and edge.weight?

▼29.2.2

What is the output of the following code?

List<WeightedEdge> list = new ArrayList<>();
list.add(new WeightedEdge(1, 2, 3.5)); 
list.add(new WeightedEdge(2, 3, 4.5)); 
WeightedEdge e = java.util.Collections.max(list);
System.out.println(e.u);
System.out.println(e.v);
System.out.println(e.weight);

Section 29.3

▼29.3.1

If a priority queue is used to store weighted edges, what is the output of the following code?

PriorityQueue<WeightedEdge> q = new PriorityQueue<>();
q.offer(new WeightedEdge(1, 2, 3.5)); 
q.offer(new WeightedEdge(1, 6, 6.5)); 
q.offer(new WeightedEdge(1, 7, 1.5)); 
System.out.println(q.poll().weight);
System.out.println(q.poll().weight);
System.out.println(q.poll().weight);

▼29.3.2

If a priority queue is used to store weighted edges, what is wrong in the following code? Fix it and show the output.

List<PriorityQueue<WeightedEdge>> queues = new ArrayList<>();
queues.get(0).offer(new WeightedEdge(0, 2, 3.5)); 
queues.get(0).offer(new WeightedEdge(0, 6, 6.5)); 
queues.get(0).offer(new WeightedEdge(0, 7, 1.5)); 
queues.get(1).offer(new WeightedEdge(1, 0, 3.5)); 
queues.get(1).offer(new WeightedEdge(1, 5, 8.5)); 
queues.get(1).offer(new WeightedEdge(1, 8, 19.5)); 
System.out.println(queues.get(0).peek()
  .compareTo(queues.get(1).peek()));

▼29.3.3

Show the output of the following code.

public class Test {
  public static void main(String[] args) throws Exception {
    WeightedGraph<Character> graph = new WeightedGraph<>();
    graph.addVertex('U');
    graph.addVertex('V');
    int indexForU = graph.getIndex('U');
    int indexForV = graph.getIndex('V');
    System.out.println("indexForU is " + indexForU); 
    System.out.println("indexForV is " + indexForV); 
    graph.addEdge(indexForU, indexForV, 2.5);
    System.out.println("Degree of U is " + 
      graph.getDegree(indexForU));
    System.out.println("Degree of V is " + 
      graph.getDegree(indexForV));
    System.out.println("Weight of UV is " + 
      graph.getWeight(indexForU, indexForV));
  }
}

Section 29.4

▼29.4.1

Find a minimum spanning tree for the following graph.

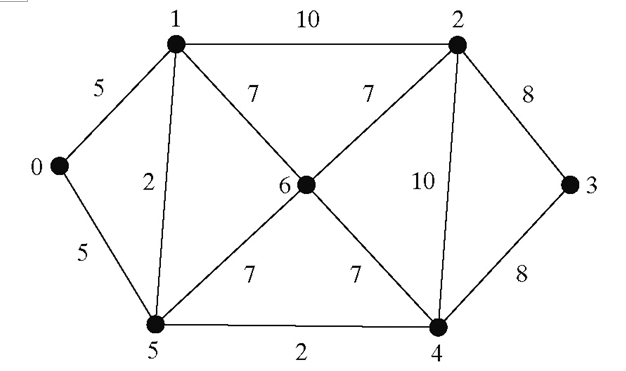
▼29.4.2

Is a minimum spanning tree unique if all edges have different weights?

▼29.4.3

If you use an adjacency matrix to represent weighted edges, what will be the time complexity for Prim's algorithm?

▼29.4.4

What happens to the getMinimumSpanningTree() method in WeightedGraph if the graph is not connected? Verify your answer by writing a test program that creates an unconnected graph and invokes the getMinimumSpanningTree() method.

▼29.4.5

Show the output of the following code:

public class Test {
  public static void main(String[] args) {
    WeightedGraph<Character> graph = new WeightedGraph<>();
    graph.addVertex('U');
    graph.addVertex('V');
    graph.addVertex('X');
    int indexForU = graph.getIndex('U');
    int indexForV = graph.getIndex('V');
    int indexForX = graph.getIndex('X');
    System.out.println("indexForU is " + indexForU); 
    System.out.println("indexForV is " + indexForV); 
    System.out.println("indexForX is " + indexForV); 
    graph.addEdge(indexForU, indexForV, 3.5);
    graph.addEdge(indexForV, indexForU, 3.5);
    graph.addEdge(indexForU, indexForX, 2.1);
    graph.addEdge(indexForX, indexForU, 2.1);
    graph.addEdge(indexForV, indexForX, 3.1);
    graph.addEdge(indexForX, indexForV, 3.1);
    WeightedGraph<Character>.MST mst 
      = graph.getMinimumSpanningTree();
    graph.printWeightedEdges();
    System.out.println(mst.getTotalWeight());
    mst.printTree();
  }
}

Section 29.5

▼29.5.1

Trace Dijkstra's algorithm for finding shortest paths from Boston to all other cities in Figure 29.1.

▼29.5.2

Is a shortest path between two vertices unique if all edges have different weights?

▼29.5.3

If you use an adjacency matrix to represent weighted edges, what would be the time complexity for Dijkstra's algorithm?

▼29.5.4

What happens to the getShortestPath() method in WeightedGraph if the source vertex cannot reach all vertieces in the graph? Verify your answer by writing a test program that creates an unconnected graph and invoke the getShortestPath() method.

▼29.5.5

If there is no path from vertex v to the source vertex, what will be cost[v]?

▼29.5.6

Assume that the graph is connected; will the getShortestPath method find the shortest paths correctly if lines 159-161 in WeightedGraph are deleted?

▼29.5.7

Show the output of the following code:

public class Test {
  public static void main(String[] args) {
    WeightedGraph<Character> graph = new WeightedGraph<>();
    graph.addVertex('U');
    graph.addVertex('V');
    graph.addVertex('X');
    int indexForU = graph.getIndex('U');
    int indexForV = graph.getIndex('V');
    int indexForX = graph.getIndex('X');
    System.out.println("indexForU is " + indexForU); 
    System.out.println("indexForV is " + indexForV); 
    System.out.println("indexForX is " + indexForV); 
    graph.addEdge(indexForU, indexForV, 3.5);
    graph.addEdge(indexForV, indexForU, 3.5);
    graph.addEdge(indexForU, indexForX, 2.1);
    graph.addEdge(indexForX, indexForU, 2.1);
    graph.addEdge(indexForV, indexForX, 3.1);
    graph.addEdge(indexForX, indexForV, 3.1);
    WeightedGraph<Character>.ShortestPathTree tree = 
      graph.getShortestPath(1);
    graph.printWeightedEdges();
    tree.printTree();
  }
}

Section 29.6

▼29.6.1

Why is the tree data field in NineTailModel in Listing 28.13 defined protected?

▼29.6.2

How are the nodes created for the graph in WeightedNineTailModel?

▼29.6.3

How are the edges created for the graph in WeightedNineTailModel?